

#Z SCORE TABLE CODE#
You can also use the above code to create Z Score Tables for values far outside the ones from the usual tables available online but usually. And voila, you have a Z Table We have successfully created a Z Score Table from scratch. For example, the z-score of 0.54 can be located along a z-table, which illustrates what percentage is under the distribution curve at any given point. Note that for z = 1, 2, 3, one obtains (after multiplying by 2 to account for the interval) the results f( z) = 0.6827, 0.9545, 0.9974, To find a specific area under a normal curve, find the z-score of the data value and use a Z-Score Table to find the area. Since it is not an easy calculation, we will be using Python to calculate it. Table of the standard normal distribution values (z 0) z 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.0 0.50000 0.50399 0.50798 0.51197 0.51595 0.51994 0.52392 0.52790 0. Rounded to the nearest hundredth, the p-value is 0.95. 07 column, and you will find the value 0.9525. Follow the chart to the place where the 1.6 on the left meets the.
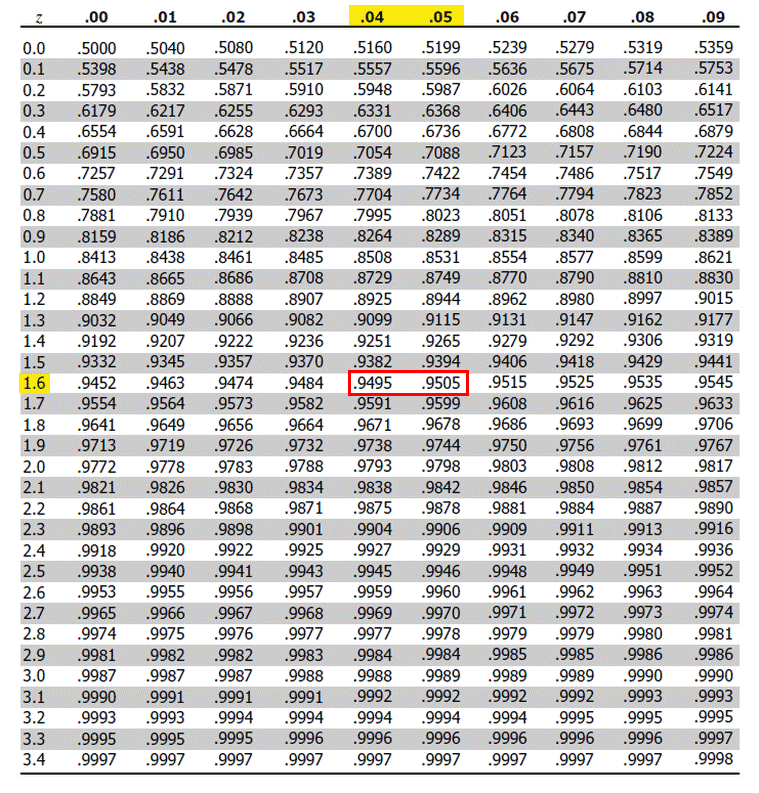
Look for 1.6 on the y-axis (left column) and. If X is a random variable from a normal distribution with mean μ and standard deviation σ, its Z-score may be calculated from X by subtracting μ and dividing by the standard deviation: Z-scores allow us to use z-tables to find the p-value.


 0 kommentar(er)
0 kommentar(er)
